三角形の円錐曲線

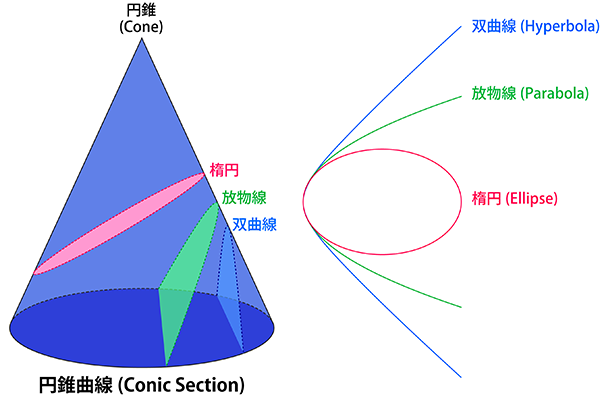
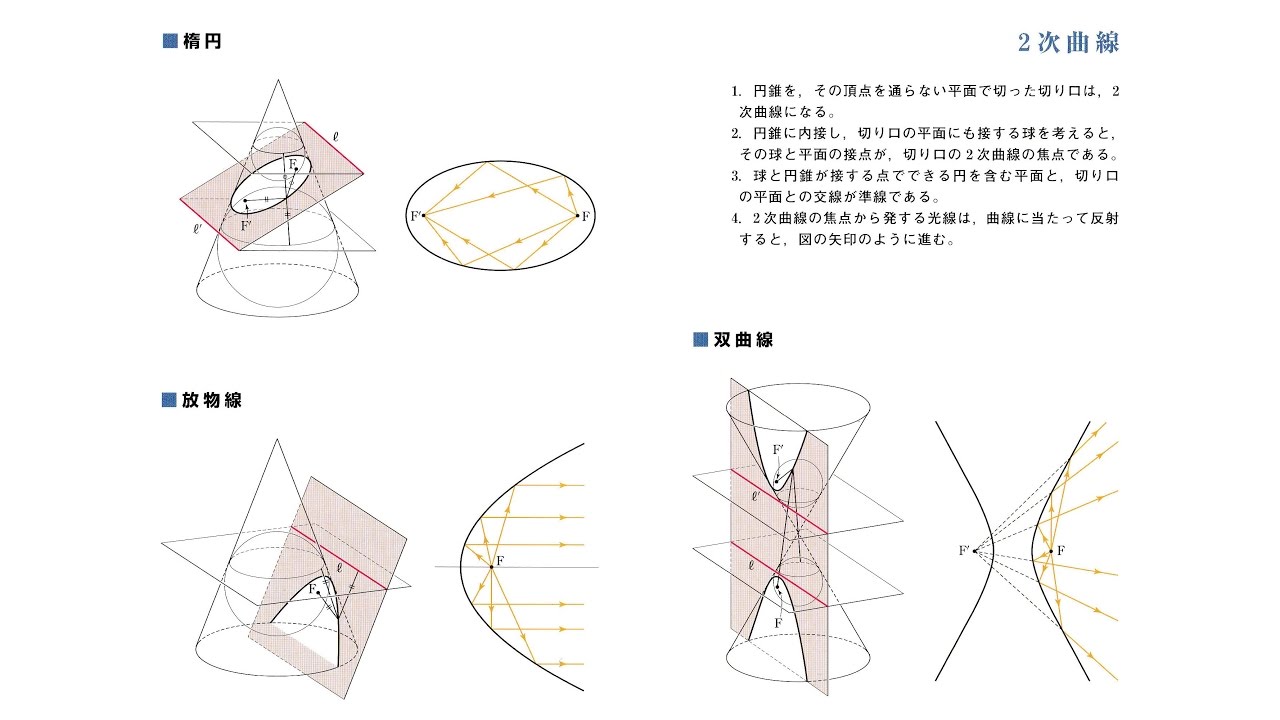
ユークリッド幾何学において、三角形の円錐曲線または三角形の二次曲線（英:Triangle conic）は三角形に定義される、円錐曲線の総称である。たとえば、外接円や内接円、シュタイナー楕円、キーペルト双曲線が挙げられる。ほかに、それぞれの頂点または対辺ごとに定義される、アルツト放物線のようなものもある。

三角形の円錐曲線と言う言葉に、明確な定義は存在せず、文献の中で広く使われている（などを参照）。ギリシャの数学者Paris Pamfilosは「円錐曲線が外接するとは、△ABCの頂点3つを通ることであり、円錐曲線が内接するとは3辺に接することである」と述べた。三角形の円、楕円、放物線、双曲線（triangle circle,ellipse,parabola,hyperbola）といった言葉も同様に定義された。

Encyclopedia of Triangle CentersやCatalogue of Triangle Cubicsのような、三角形に対する図形の辞典のようなもので、円錐曲線がまとめられているものは2024年現在、存在しない。

三線座標による式

三線座標x : y : zを用いて任意の円錐曲線は以下の式で表される。 $rx^{2} sy^{2} tz^{2} 2uyz 2vzx 2wxy=0.$ うち、外接円錐曲線と内接円錐曲線は以下の式で表すことができる。 ${\begin{aligned}&uyz vzx wxy=0\\[2pt]&l^{2}x^{2} m^{2}y^{2} n^{2}z^{2}-2mnyz-2nlzx-2lmxy=0\end{aligned}}$

特別な三角形の円錐曲線

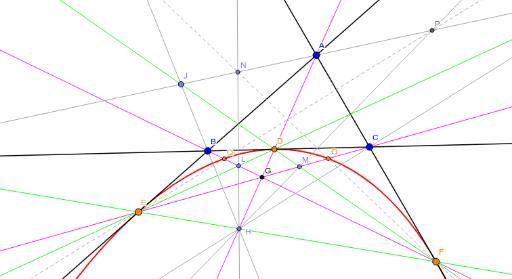
以下に有名な円錐曲線を挙げる。基準となる三角形を△ABC 、頂点及び角をA, B, C、その対辺をそれぞれa, b, c、とする。また、円錐曲線をあらわす三線座標の変数をx : y : zとする。

三角形の円

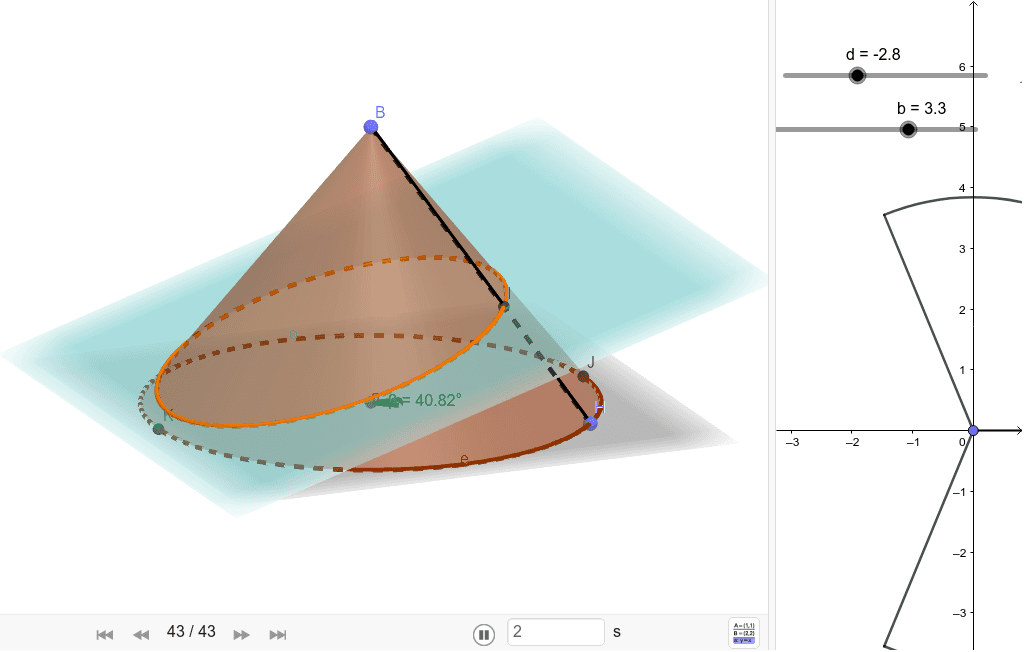
三角形の楕円

三角形の双曲線

三角形の放物線

三角形の円錐曲線の族

ホフスタッター楕円

ホフスタッター楕円（Hofstadter ellipses）はある媒介変数によってあらわされる楕円の集合である。 $x^{2} y^{2} z^{2} yz\left[D(t) {\frac {1}{D(t)}}\right] zx\left[E(t) {\frac {1}{E(t)}}\right] xy\left[F(t) {\frac {1}{F(t)}}\right]=0$ ただし t は媒介変数で ${\begin{aligned}D(t)&=\cos A-\sin A\cot tA\\E(t)&=\cos B-\sin B\cot tB\\F(t)&=\cos C-\sin C\cot tC\end{aligned}}$ である。 t と 1 − t が表す楕円は等しい。また t = 1/2のとき内接楕円 $x^{2} y^{2} z^{2}-2yz-2zx-2xy=0$ となり t → 0とすると外接楕円 ${\frac {a}{Ax}} {\frac {b}{By}} {\frac {c}{Cz}}=0.$ となる。

トムソン円錐曲線とダルブー円錐曲線

トムソン円錐曲線（Thomson Conics）は、各辺との接点を通る、各辺の法線が共点である内接円錐曲線の集合である。ダルブ―円錐曲線（Darboux Conics）は頂点での円錐曲線の法線が共点である外接円錐曲線である。双方の共点は、ダルブ―三次曲線上にある。

平行線との交点により構成される円錐曲線

△ABCと点Pについて、Pを通るBC,CA,ABに平行な線と、他2辺との交点をそれぞれX_b, X_c, Y_c, Y_a, Z_a, Z_bとする。この6点は同一円錐曲線上にある。特にPが類似重心であるとき円となる。Pの三線座標をu:v:wとすると、6点を通る円錐曲線は以下の式で表される。 $-(u v w)^{2}(bcuyz cavzx abwxy) (ax by cz)(vw(v w)ax wu(w u)by uv(u v)cz)=0$

九点円錐曲線

△ABCと点Pについて、AB,BC,CA,AP,BP,CPの中点と、AB,CP、BC,AP、CA,BPの交点の計9点を通る円錐曲線を九点円錐曲線（Nine-point conic）という。Pが垂心のとき円（九点円）、重心のとき内接楕円（シュタイナーの内接楕円）となる。

イフ円錐曲線

媒介辺数 $\lambda$ を用いて、 $x^{2} y^{2} z^{2}-2\lambda (yz zx xy)=0,$ で表される円錐曲線をイフ円錐曲線（Yff conics）という。任意の点P(u : v : w)によって $\lambda$ は $\lambda ={\frac {u^{2} v^{2} w^{2}}{2(vw wu uv)}}.$ で表される。特に放物線（イフ放物線、Yff parabola）の時は $\lambda ={\frac {a^{2} b^{2} c^{2}}{a^{2} b^{2} c^{2}-2(bc ca ab)}}=\lambda _{0}$ である。

$\lambda <\lambda _{0}$ または $\lambda >{\frac {1}{2}}$ のとき楕円、 $\lambda _{0}<\lambda <-1$ のとき双曲線となる。 $-1<\lambda <{\frac {1}{2}}$ のときは、座標平面上には表れない。

ラビノヴィッツ円錐曲線

△ABCと点Pについて、同じ向きにAP//BD//CE,BP//CG//AF,CP//AH//BIで、AP=AF=AH,BP=BD=BI,CP=CE=CGを満たすように点D,E,F,G,H,Iをとると、その6点は同一円錐曲線上にある。これをラビノヴィッツ円錐曲線（Rabinowitz Conics）と言う。